三角関数の極限公式は以下3つ。
三角関数の極限公式[math] \lim_{x \rightarrow 0} \dfrac{\sin x}{x} =1 [/math] ・・・・ (ⅰ)
[math]\lim_{x \rightarrow 0} \dfrac{\tan x}{x} =1[/math] ・・・・(ⅱ)
[math]\lim_{x \rightarrow 0} \dfrac{1 – \cos x}{ x^{2} } = \dfrac{1}{2}[/math] ・・・・(ⅲ)
数学の問題を解くには案外公式の暗記が必要となる。
これは覚えておくべき公式の一つである。
また、(ⅰ)の証明は図形的にできるので以下に示す。
(ⅰ)の証明
これは三角形の面積・扇形の面積から図形的に証明できる。
半径1、中心角 [math]x[/math]([math]0 < x < \dfrac{ \pi }{2} [/math])から考えられる2つの三角形、及び扇形の面積について考える。
●中心角 [math]x[/math]([math]0 < x < \dfrac{ \pi }{2} [/math])、その核をなす2つの辺1の面積[math]S_{1} [/math]
[math]S_{1} = \dfrac{1}{2}[/math]・1・1・[math]\sin x[/math]
ここで1・[math]\sin x[/math]は……
∠bac=xとなる三角形の底辺acとbから垂直に交わる交点をdとすると
[math]\dfrac{bd}{ab} = \sin x[/math]
[math]bd = ab \sin x[/math]
●中心角[math]x[/math]([math]0 < x < \dfrac{ \pi }{2} [/math])、半径1の扇形の面積[math]S_{2} [/math]
円と角度xをなす扇形の角度と面積の比より
[math]r^{2} \pi : S_{2}= 2 \pi : x[/math]
[math]2 \pi S_{2} =x r^{2} \pi [/math]
[math]S_{2} = [/math][math]\dfrac{1}{2} x r^{2} [/math]
●中心角 [math]x[/math]([math]0 < x < \dfrac{ \pi }{2} [/math])、底辺1、高さ[math]\tan x[/math]の面積[math]S_{3} [/math]
[math]S_{3} = \dfrac{1}{2}[/math]・1・[math]\tan x[/math]
=[math]\dfrac{1}{2}\tan x[/math]
3つの面積の大小関係は[math]S_{1} \leqq S_{2} \leqq S_{3}[/math]なので
[math]\dfrac{1}{2}\sin x \leqq \dfrac{1}{2} x \leqq \dfrac{1}{2} \tan x[/math]
[math]\sin x \leqq x \leqq \dfrac{\sin x}{\cos x} [/math] ([math]0 < x < \dfrac{ \pi }{2} [/math])
[math]x > 0[/math], [math]\cos x>0[/math] なので
[math]\sin x \leqq x[/math] より
[math] \dfrac{\sin x}{x} \leqq 1[/math]
また [math]x \leqq \dfrac{\sin x}{\cos x} [/math] より
[math]\cos x \leqq \dfrac{\sin x}{x} [/math]
よって
[math]\cos x \leqq \dfrac{\sin x}{x} \leqq 1[/math]
[math]\lim_{x \rightarrow 0} \cos x \leqq \lim_{x \rightarrow 0} \dfrac{\sin x}{x} \leqq 1[/math]
[math]\lim_{x \rightarrow 0} \cos x = 1[/math] なので
はさみ打ちの原理より
(ⅱ)の証明
続いて(ⅱ)の証明は上で証明した(ⅰ)を用いることで証明可能。
[math]\lim_{x \rightarrow 0} \dfrac{\tan x}{x} = \lim_{x \rightarrow 0} \dfrac{1}{x} ・\dfrac{\sin x}{\cos x} [/math]
[math]= \lim_{x \rightarrow 0} \dfrac{\sin x}{x} ・ \dfrac{1}{\cos x} [/math]
=1・1 = 1
よって
(ⅲ)の証明
この証明も(ⅱ)の証明同様、上で証明した(ⅰ)を用いることで証明可能。
[math]\lim_{x \rightarrow 0} \dfrac{1-\cos x}{ x^{2} } = \lim_{x\rightarrow 0} \dfrac{(1-\cos x)(1 + \cos x)}{ x^{2}(1 + \cos x) } [/math]
[math]= \lim_{x\rightarrow 0} \dfrac{(1-\ cos ^{2}x )}{ x^{2}(1 + \cos x) } [/math]
[math]= \lim_{x\rightarrow 0} ( \dfrac{\sin x}{x} )^{2} ・ \dfrac{1}{1 + \cos x} [/math]
上で証明した三角関数の極限公式(ⅰ)より
[math]\lim_{x \rightarrow 0} \dfrac{\sin x}{x} = 1[/math] なので
[math]=1・ \dfrac{1}{2} =\dfrac{1}{2}[/math]
よって

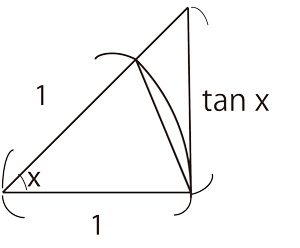


コメント